Assignments for CS 216, Fall 2024

Preliminaries

Implement the B-Tree data structure which supports the methods given below.

Create project BTree that has class BTree. All classes for this assignment should be put in separate files. Unlike the previous assignments, class Node should be generic and should always be referred to as Node<E> in the code.

Use ArrayList and use this as guide about the approprtiate type of loop.

Visualization resources

Here is a useful visualization resource:

USFCA Visualization -- note that its meaning of L is max children allowed (for us L is max items allowed)

JUnit

Copy to your Tester the contents of the following file and make the relevant updates/changes:

BTreeTest.java

See method toString at the end for the expected string format.

The style and general expectations are the same as in Assignments 5 and 6.

the private methods (those that return Node or take Node as parameters) will be tested implicitly, by the corresponding public methods, so do not write test cases for the private methods; for example, contains implicitly tests findNode
you only need to write test cases for the BTree class and only for the public, i.e. non-Node, methods.

Node Class (Part I: Add, Contains, Inorder)

Make this an external, generic class (unlike the Nodes for BSTree and DLinkedList, which were internal classes).

The Node class has the following data members:

data members will be default as other Node classes, but avoid direct access to these members from other classes when possible
the order L of the node: a non-root node must contain at least L/2 and at most L data items (the minimum requirement does not apply to a root node, the one without a parent)
a pointer to the parent node
a comparator object that implements the Comparator interface: this object will be used to compare the values in the node (see Comparator)
a collection of data items and a collection of children pointers: if a non-leaf node has k data items, it must have k+1 children (leaf nodes contain data, but have no children)

The Node class has the following methods:

Node(int theOrder, Comparator<E> theComp)

Creates an empty node of the given order and the given comparator.

Node(int theOrder, Comparator<E> theComp, Node<E> left, E item, Node<E> right)

Creates a node with the given left and right children and the single separator data item for the children.

Node(int theOrder, Comparator<E> theComp, Node<E> theParent, ArrayList<E> theData, ArrayList<Node<E>> theChildren)

Creates a node with the given parent p, data items, and children.

boolean hasOverflow()

Determines if this node is filled beyond capacity (and needs to be split).

boolean isLeaf()

Determines if this node is a leaf.

Node<E> childToFollow(E item)

Returns the next child to follow down the tree in order to locate the given item.
[ this is useful for traversing the tree to find the leaf where the item would be inserted ]
Think of the given item as a rolling ball over the items in the node. When the rolling ball hits a larger item, it chooses to go down the arrow/child to the left side of that large item.

void leafAdd(E item)

Inserts the given item in the correct position among this node's data items.
[ this is intended to be used with leaf nodes only; no checks needed ]

void split()

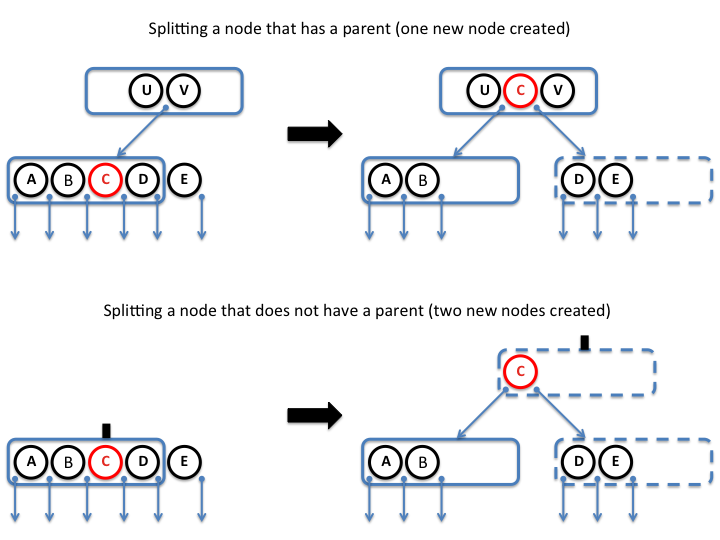
Splits this node by creating a new right sibling node. The new sibling is given half of this node's data items and half of the children. The original middle value of this node is promoted to this node's parent and the new sibling is inserted in this node's parent behind the middle value. No loops.

Mthod indexOf(...) can be used to find the index of this node (the one being split) among its parent's children.
Method subList(int from, int to) can be used to retrieve a portion of a list data structue (check the API for meaning of from and to). Note that you also need to use clear() to remove that portion from the original list.
// transfer a range from one list to another -- copy+clear
myList = new L.L.( yourList.subList(from, to) );
yourList.subList(from, to).clear();
No loops.

boolean contains(E item)

Determines if this node contains the given item.

BTree Class (Part I: Add, Contains)

The BTree class has the following data members:

a pointer to the root of the tree: the root is never null, it starts as an actual node
a comparator object to be used to order the items in the tree (same meaning as the Node class)
the order L of the tree (same meaning as the Node class)

The BTree class has the following methods:

BTree(int theOrder, Comparator<E> theComp)

Creates an empty tree of the given order and the given comparator.

void add(E item)

Adds the given item to the tree. See INSERT Algorithm below.

Node<E> findLeaf(Node<E> curr, E item)

(non-recursive) Finds the leaf node in the tree rooted at the given node curr where the given item should be inserted.

boolean contains(E item)

Determines if the tree contains the given item (see findNode).

Node<E> findNode(Node<E> curr, E item)

(recursive) Finds the node that contains the given item in the tree rooted at the given node curr.

void inorder(Consumer<E> consumer)

Performs inorder traversal of this tree (see next method). Recall that inorder traversal visits the items in sorted order.
No need to write test cases for this method. It will be tested implicitly via toStringSorted.

void inorder(Consumer<E> consumer, Node<E> curr)

(recursive) Performs inorder traversal of the tree rooted at the given node curr.
This is a generalization of the inorder traversal of a BSTree:

for BSTree the inorder traversal was:

traverse child 1 (the left), visit item, traverse child 2 (the right)

for BTree the inorder traversal is:

traverse child 1, visit item 1, traverse child 2, visit item 2, traverse child 3, .... and so on

String toStringSorted()

Returns a string representation of this tree in sorted order.
This method simply calls void inorder(Consumer<E> consumer) with the StringConsumer from Assignment 6 (copy relevant classes to this project).
Tree with L=4:                       String representation:
   
     [ 10      20 ]                  [5 8 10 12 18 20 23 36 40]
     /      |      \                 
[5 8]    [12 18]  [23 36 40]

String toString()

Returns a string representation of this tree in level-order traversal in this format ([[]] for empty tree):
Tree with L=4:                       String representation:
   
     [ 10      20 ]                  [[10 20] [5 8] [12 18] [23 36 40]]
     /      |      \                  -lvl=1- ---------lvl=2---------- ---etc.---
[5 8]    [12 18]  [23 36 40]
Initially, could use the following method (download btreeutils.jar, "right-click, Save As..." and see Assignment 5):
public String toString()
{
    return new BTreeUtils<E>().toString( your-root );
}
Adapt the BSTree Level Order Iterator from Assignment 5. Recall that we discussed a while-loop version of BSTree Level Order which was split in various pieces and the pieces were put in various iterator methods.
Here we put those pieces back together into the loop method. Conceptually, the main difference between B-Tree and BStree is that we insert many children in the queue at each step, not just two. Essentially allmost all of the code from the iterator is placed directly here, in method toString, with appropriate changes.
Only one loop. Note that you can write:
str = str + list_of_stuff;

To remove the commas at the end:

str = str.replaceAll(",", "")

INSERT Algorithm

Here is the pseudocode for the BTree class INSERT operation:

find the leaf node where the item should be inserted

add the item to the leaf node

start from the leaf node moving up towards the root

as long as current node is full, split current node and move up

final adjustments, if necessary

REMOVE Algorithm

Here is the pseudocode for the BTree class REMOVE operation:

find the node that contains the given item

if the node is a leaf:

remove the item from this node's data list

repair the tree starting at this leaf node

if the node is internal:

find the max node, i.e. the node with the largest value, in the subtree to the left of the given item

remove the largest value from the max node and use it to replace the given item in the node found in step 1.

repair the tree starting at the max node (must be a leaf leaf node)
[ Note: Steps i. and ii. are the same as in the remove method in a Binary Search Tree. ]

REPAIR Algorithm

Here is the pseudocode for the BTree class REPAIR operation:

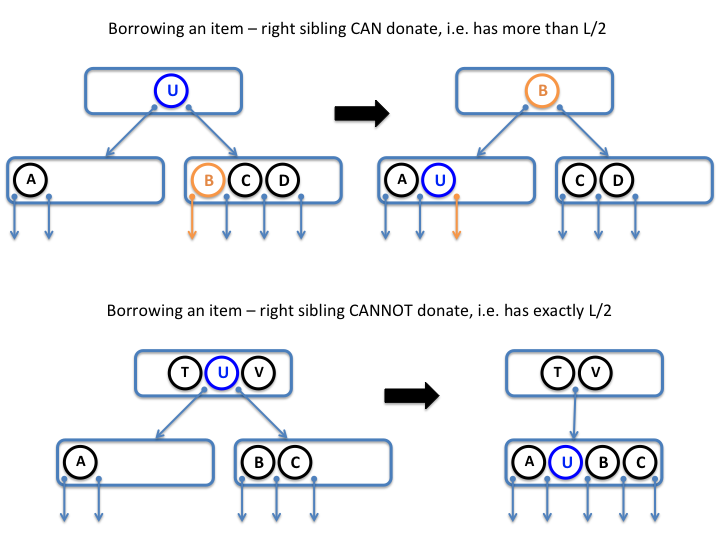start from the given leaf node moving up towards the root

as long as current node is deficient, let the current node borrow from a sibling

final adjustments, if necessary

CS 216
Data Structures and Algorithms

Assignment 8

Preliminaries

Visualization resources

JUnit

Node Class (Part I: Add, Contains, Inorder)

BTree Class (Part I: Add, Contains)

INSERT Algorithm

REMOVE Algorithm

REPAIR Algorithm

CS 216 Data Structures and Algorithms

Assignment 8

Preliminaries

Visualization resources

JUnit

Node Class (Part I: Add, Contains, Inorder)

BTree Class (Part I: Add, Contains)

INSERT Algorithm

REMOVE Algorithm

REPAIR Algorithm

CS 216
Data Structures and Algorithms