CS 112 - Introduction to Computer Science II Homework #3

1. Catalan Numbers: Catalan Numbers show up in many combinatorics counting problems, e.g. the number of binary trees that have n internal nodes (i.e. n + 1 terminal nodes).  In Catalan.java, create a method public static long c(int n) that recursively computes Catalan number C_n for n >= 0 according to the following definition:

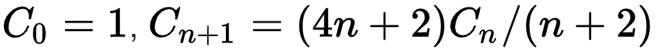
Hint: It would be beneficial to rewrite the recursive step in terms of C_n by replacing the right-hand side occurrences of n with n - 1.
Optional challenge: The method body of Catalan.c can be expressed as a single statement.

2. Counting Non-Pig Roll Sequences:  The game of Pig is a very simple jeopardy dice game in which two players race to reach 100 points. Each turn, a player repeatedly rolls a die until either a 1 (called a “pig”) is rolled or the player holds and scores the sum of the rolls (i.e. the turn total). At any time during a player's turn, the player is faced with two decisions:

• roll - If the player rolls a
  • 1 (“pig”): the player scores nothing and it becomes the opponent's turn.
  • 2 - 6: the number is added to the player's turn total and the player's turn continues.
• hold - The turn total is added to the player's score and it becomes the opponent's turn.

For this problem, in PigRollSequences.java you will implement method public static int getNumSequences(int turnTotal) that recursively computes and returns how many different possible non-pig roll sequences (i.e. roll sequences without 1s) result in a turn total of k, where 0 <= k <= 50.  For example, there are 5 possible roll sequences that result in a turn total of 6: 2-2-2, 2-4, 3-3, 4-2, and 6.  Note that 2-4 and 4-2 count as distinct roll sequences; you are not counting roll sets.  Note also that the empty sequence leads to a turn total of 0 at the beginning of your turn, i.e. getNumSequences(0) == 1 .

For k = 2, 6, and 10, your result should be 1, 5, and 29, respectively.

Hint 1: The number of roll sequences leading to turn total k is the sum of the number of roll sequences leading to k-2, k-3, ..., and k-6

Hint 2: Dynamic programming should be used to speed computation.

3. Toads and Frogs: Read about the game of Toads and Frogs.  The game is played on a single row of n positions, each of which contains a toad, a frog, or is empty.  Toads/frogs are played by the toad/frog player and always move/hop rightward/leftward, respectively.  On a turn, the toad/frog player may either (1) move a toad/frog into a right-/left-adjacent frog/toad into an empty position, or (2) hop a single toad/frog over a right-/left-adjacent frog/toad into an empty position immediately beyond, respectively.

The toad player plays first, and turns alternate.  The first player unable to make a move loses.  Here is an example game with T's representing toads, F's representing frogs, and dashes representing empty spaces:

TT---FF
T (toad player) moves right.
T-T--FF 
F (frog player) moves left.
T-T-F-F
T could move either toad but chooses to move the foremost.
T--TF-F
F could hop or move, and chooses to move.
T--TFF-
T can only move.
-T-TFF-
F must hop.
-TFT-F-
T must move.
-TF-TF-
F could hop either frog and choose to hop the hindmost.
-TFFT--
T must move.
-TFF-T-
F must hop.
FT-F-T-
T could move either toad but chooses to move the hindmost.
F-TF-T-
F must hop.
FFT--T-
T could move either toad but chooses to move the hindmost.
FF-T-T-
F cannot move/hop and thus loses the game.

This initial board position was a guaranteed win for the toad player (T) with perfect play.  That is not to say that T could not have lost the game with poor play:

TT---FF
T-T--FF
T-T-F-F
-TT-F-F
-TTF--F
-T-FT-F
-TF-T-F
--FTT-F
--FTTF-
--FT-FT
--FTF-T
--F-FTT
--FF-TT
And T cannot move/hop and thus loses the game.

For this assignment, you will implement a recursive solver to determine which player will win the game with perfect play in a given situation.

We will represent a game state as (1) a character array containing toads ('T'), frogs ('F'), and empty spaces ('-'), and (2) the current player ('T'/'F').  In ToadsAndFrogSolver.java, given a game state as separate parameters, you will implement method public static char getWinner(char[] board, char currentPlayer) that takes in a game state and returns which player will win if both players play perfectly.

The recursive algorithm is sketched is as follows: (A more detailed sketch is given  below, but see if you can work this algorithm without that sketch.)

• For each legal move for the current player,
  • If we call getWinner on the resulting game state (new board, other player) and find that this leads to a win for the current player, then return the current player.
• Otherwise, failing to find a winning play (or any legal play), return the opponent player.

You are encouraged to begin with this ToadsAndFrogsSolver.java starter code which includes a main method for testing.

Note 1: Before and after a call to getWinner(char[] board, char currentPlayer), the contents of char[] board should remain unchanged.

Note 2: While dynamic programming would speed computation, we will test with small enough game boards so that the implementation of dynamic programming is optional.

Example transcripts (input underlined):

Board position (using TF-)? T-F
Current player (T/F)? T
Winner: T

Board position (using TF-)? T--F
Current player (T/F)? T
Winner: F

Board position (using TF-)? TTT-FFF
Current player (T/F)? T
Winner: T

Board position (using TF-)? TTF-TF-F
Current player (T/F)? T
Winner: F

More detailed pseudocode:

getWinner(board, current player):

• for each board position:
  • if the current player is 'T' and a 'T' is at this position:
    • if a move is not out of bounds and there is an empty space to the right:
      • make the move in the board
      • char winner = getWinner(board, 'F')
      • unmake the move in the board
      • if winner == current player, return current player
    • if a hop is not out of bounds and there is a 'F' to the right and a '-' to the right of that:
      • ... (same structure as with move)
• else (the current player is 'F' and 'F' is at this position):
  • ... (same structure as with current player 'T')
• return opponent player  (Note: We only reach this point if either (BASE CASE) no legal moves were found, or (RECURSIVE CASE) all legal moves were wins for the opponent.)

This is only one correct structure for a correct recursive evaluation.  Any recursive evaluation is allowable.

Rubric: (20 points total)

• 5 points: Catalan numbers (must be recursive; -3 points for an iterative implementation)
• 5 points: Counting Non-Pig Roll Sequences (must be recursive; -3 points for an iterative implementation)
• 10 points: Toads and Frogs (must be recursive; -5 points for an iterative implementation)

Note by "iterative implementation", we mean an entirely iterative implementation with no recursion.  Even recursive implementations for "Counting Non-Pig Roll Sequences" and "Toads and Frogs" will have iteration through different roll values and board positions, respectively.  The key here is to solve each problem through recursive calls to smaller/simpler problems of the same type.  Don't overthink your recursion; cover the base case(s) and, for recursive cases, think only one step ahead at most.