CS 371 - Introduction to Artificial Intelligence
Homework #3

Due: Thursday 10/10 at the beginning of class
Note: Work is to be done in pairs

Simulated Annealing

HW3 Code Resources

1. The Channel Routing Problem (CRP):

For this exercise, you'll be given an Annealable class by C.S. major David Hettlinger from his research of summer 2002. This class implements a complex combinatorial optimization problem concerning VLSI circuit design. For this "Channel Routing Problem", horizontal and vertical wires are on opposite side of and connected through a silicon wafer. We seek to find a wiring layout between pins with corresponding numbers that minimizes the number of necessary horizontal tracks. All implementation of the Annealable interface is supplied for you. Your task is to implement and collect data on optimization performance with 10000 iterations for:

iterative improvement with 0%, 10%, 20%, 40%, and 100% uphill step acceptance, and
simulated annealing with an initial temperature of 70 and a temperature decay of .95 per iteration.

Construct each initial CRP state with "new CRState4("dde.txt")". All other interaction with this class will be according to the Annealable interface. Record the final energy (i.e. channel width) for each optimization run, and perform a minimum of 3 runs for each method/setting above (i.e. minimum 18 runs total). We will share results for this problem on Tuesday 10/8 in class.

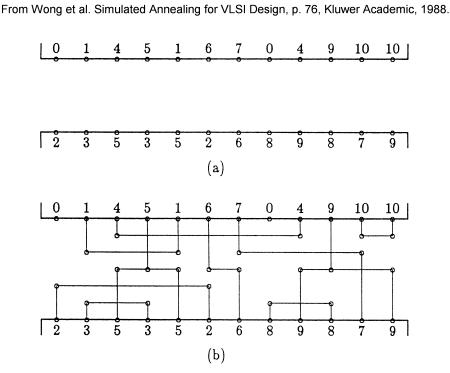
2. Scheduling Problem: Apply simulated annealing to the following problem: Given a number of students wishing to take a number of classes which can be assigned to a number of time slots, assign classes to time slots in such a way as to minimize schedule conflicts. You will create a class SchedulingProblem which implements Annealable. Its constructor will take a number of students, the number of classes a student takes, a number of classes offered, and a number of time slots (e.g. 240 students with 5 classes each, 100 classes offered, 12 time slots). Each randomly generated instance of the problem will associate each student with the given number of different random classes. Each class will be associated with a random time slot. For the purposes of the Annealable interface, next causes a class to be randomly reassigned to a different time slot. Energy is the sum of the student conflicts. The number of conflicts for a student is the number of their classes they cannot attend given the current schedule. (For the example above, if all of a student's classes are scheduled at the same time, the student has 4 conflicts.)

With parameters that generate problems which will likely not have a zero-conflict schedule, demonstrate the performance of simulated annealing versus iterative improvement with only downhill steps.

Todd Neller