
 |
FairKalah: Fair Mancala |

Kalah, usually called "Mancala" in the United States, is a Mancala game variant invented in 1940 by William Julius Champion and patented in 1955 as US Patent 2,720,362. In the Mancala games family, it is most closely related to Dakon from Java. Kalah has enjoyed popularity in the United States and Germany through its history.
However, Kalah has what could be considered a design flaw: A game between two perfect players results in a first-player win by 10 points. With only 48 points to be scored, this represents a significant first-player advantage. While human players could not be expected to play perfectly, those familiar with Kalah usually know the optimal first plays that put the second player on the defensive from the start: The move four pits away from the scoring pit (resulting in a free move) followed by the move next to the scoring pit (resulting in a capture threat to the second player).
FairKalah is Kalah played from a fair starting position. Below, we reiterate the rules of Kalah/Mancala, share fair starting positions that can be easily set up by moving 1 or 2 pieces from the standard starting position, and share further resources about the game.
Video presentation of the rules (5:52) and a complete demonstration game (6:20)
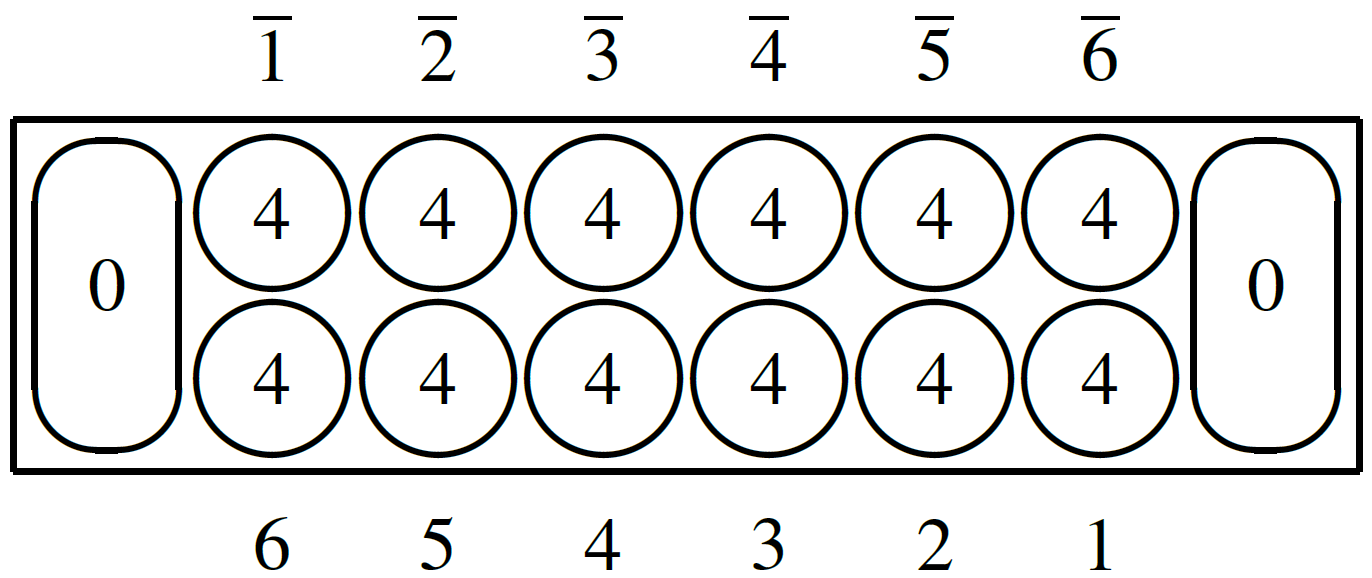
Materials: Mancala (a.k.a. Kalah) is played on a rectangular board as depicted above with 6 play pits for each player along the long side and 1 score pit ("Kalah") for each player on the player's right-hand end of the board. In the standard initial board state, each of the play pits starts with 4 pieces (a.k.a. seeds) per pit. We refer to play pits by the number of pits they are clockwise away from the player's score pit. (Pits of the second player (north) are notated with overbars. Numbers depicted within pits indicate the number of pieces in that pit.)Play: On a player's turn, the player selects one of their play pits containing pieces, removes all pieces from that play pit, and redistributes ("sows") them counterclockwise, one piece per play/score pit, and skipping their opponent's score pit. If the last piece redistributed lands in the score pit, the player takes another turn; otherwise, it becomes the opponent's turn. If the last piece redistributed lands in an empty play pit of the player (including after having redistributed pieces to all opponent play pits), then that piece captures: both that piece and any pieces in the opponent's opposite play pit are removed from the pits and placed into the player's score pit.
Game End: The game ends when, at the end of a turn, there are no pieces left in one player's play pits. Their opponent scores any remaining pieces in play pits. The player with more pieces in their score pit wins. If the number of pieces in the score pits are the same, the players draw (i.e. tie) the game.
One can observe example game play with this plain text game transcript. Note how we interpret the original patent rules with regards to the final "empty capture" or "zero capture". The original rule text of both the patent and the 1958 Kalah Game Company rules have only the "if" condition that the last piece lands in a player's empty play pit. There appears to be no requirement that there be opponent pieces to capture. This is consistent with the research interpretation of Irving, Donkers, and Uiterwijk. Without this empty/zero-capture rule, the last move taken would not result in a capture.
It is also worth noting that the last move leaves the first player's side empty, yet the opponent has a legal move. In some variants, the game ends when the a player has no legal moves on their turn, which is known as "starvation". As one can see in this transcript, if we didn't end the game when either player's play pits are empty, then the second (north) player's turn would necessarily redistribute pieces to the first (south) player's play pits. Both the original patent rules and the 1958 Kalah Game Company rules clearly end the game "when all of the pits on one side of the game board are empty" and "when all six pits on one side are empty", respectively.
Here are the three FairKalah boards that can be set up by starting with a standard 4-piece-per-play-pit starting position and moving a single piece:
There are 251 FairKalah starting positions that one can create by moving 2 pieces from the standard starting position. All 254 FairKalah starting positions that can be created by moving 1 or 2 pieces are depicted here. These positions are also available in comma-separated value (CSV) format where each row lists the number of pieces in each pit, starting with the first players leftmost play pit and proceeding counter-clockwise around the board (including score pits).
These fair initial states were found by computing the game value of each possible redistribution of one or two pieces and retaining only those with a game value of 0 (draw). Initial state evaluations were performed with our Java port of Geoffrey Irving's Mancala analysis code used for the paper Solving Mancala featuring zero-window alpha-beta search and a 24-piece endgame database we computed. FairKalah was developed as a collaboration between Todd W. Neller and Taylor C. Neller.