Recursive Best-First Search (Korf, 1993)

RBFS (node: N, value: F(N), bound: B)

IF f(N)>B, RETURN f(N)

IF N is a goal, EXIT algorithm

IF N has no children, RETURN infinity

FOR each child Ni of N,

IF f(N)<F(N), F[i] := MAX(F(N),f(Ni))

ELSE F[i] := f(Ni)

sort Ni and F[i] in increasing order of F[i]

IF only one child, F[2] := infinity

WHILE (F[1] <= B and F[1] < infinity)

F[1] := RBFS(N1, F[1], MIN(B, F[2]))

insert Ni and F[1] in sorted order

RETURN F[1]

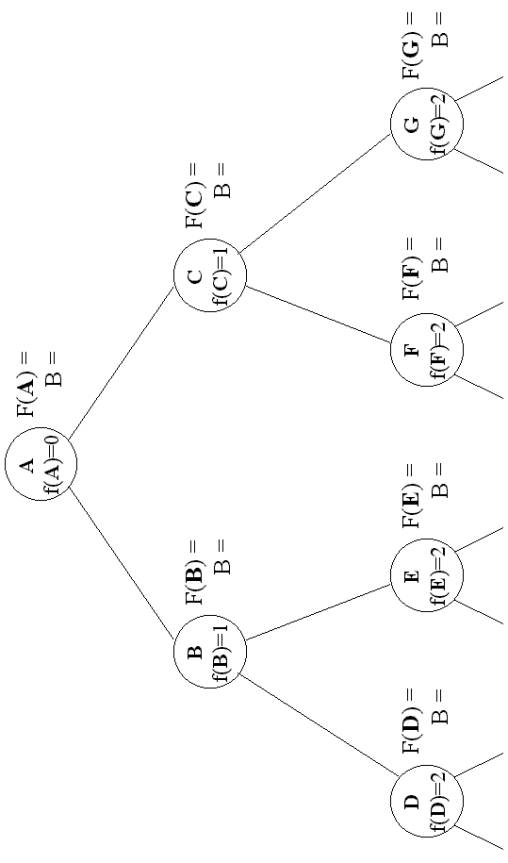
Korf illustrated the workings of this algorithm with a binary tree where f(N) = the depth of node N. What follows is a brief, structured description of how the algorithm works in this case. It is best to try to work the algorithm on your own on paper and use this as a reference to check your work. Nodes in the binary tree are named A, B, C, … from left-to-right, top-to-bottom. Assume the tree is infinite and has no goal. Note that the stored value F(N) is different from f(N). When sorted children are listed (e.g. “B(1) C(1)”), the number inside the parentheses is the stored value. Recursive calls are indented; the first line is the initial call on the root.

RBFS(A, 0, 4)

f(A)=F(A), so F(B)=f(B)=1, F(C)=f(C)=1

Sorted children: B(1) C(1)

F(B)< 4, so

RBFS(B, 1, 1)

f(B)=F(B), so F(D)=f(D)=2, F(E)=f(E)=2

Sorted children: D(2) E(2)

F(D)>1, so return 2

F(B)=2

Sorted children: C(1) B(2)

F(C)< 4, so

RBFS(C, 1, 2)

f(C)=F(C), so F(F)=f(F)=2, F(G)=f(G)=2

Sorted children: F(2) G(2)

F(F)<=2, so

RBFS(F, 2, 2)

… search F’s children to 2 returning min cost beyond …

return 3

F(F)=3

Sorted children: G(2) F(3)

F(G)<=2, so

RBFS(G, 2, 2)

… search G’s children to 2 returning min cost beyond …

return 3

F(G)=3

Sorted children: F(3) G(3)

F(F)>2, so return 3

F(C)=3

Sorted children: B(2) C(3)

F(B)< 4, so

RBFS(B, 2, 3)

f(B)<F(B), so F(D)=MAX(F(B),f(D))=2,

F(E)=MAX(F(B),f(E))=2

Sorted children: D(2) E(2)

F(D)<=3, so

RBFS(D, 2, 2)

… search D’s children to 2 returning min cost beyond …

return 3

F(D)=3

Sorted children: E(2) D(3)

F(E)<=3, so

RBFS(E, 2, 3)

… search E’s children to 3 returning min cost beyond …

return 4

F(E)=4

Sorted children: D(3) E(4)

F(D)<=3, so

RBFS(D, 3, 3)

… search D’s children to 3 returning min cost beyond …

return 4

F(D)=4

Sorted children: E(4) D(4)

F(E)>3, so return 4

F(B)=4

Sorted children: C(3) B(4)

F(C)< 4, so

RBFS(C, 3, 4)

… search C’s children to 4 returning min cost beyond …

return 5

F(C)=5

Sorted children: B(4) C(5)

F(B)< 4, so

RBFS(B, 4, 5)

… search B’s children to 5 returning min cost beyond …

return 6

F(B)=6

Sorted children: C(5) B(6)

… and so on …