Slide 7 of 19
Notes:
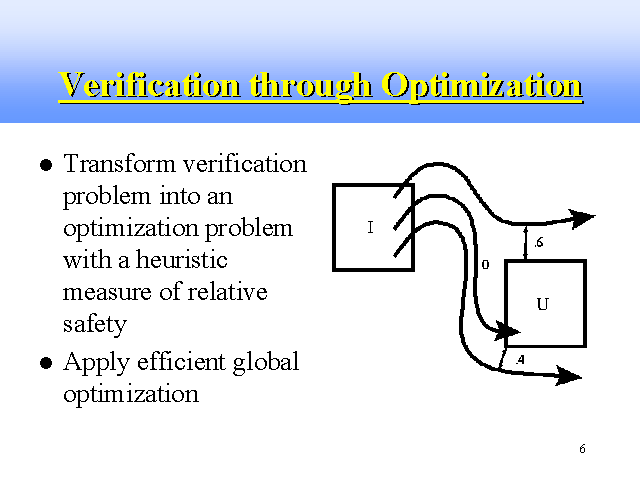
More generally, let us consider what we've done here: Given a set of initial states I, a set of unsafe states U, and a bounded initial time interval, we wish to know if there exists a simulated trajectory from I to U within that interval. To this end, we apply our problem domain knowledge to create a function f which takes initial conditions as input, simulates the system, and outputs 0 if and only if the trajectory leads from I to U, and otherwise outputs a positive heuristic rating of the relative safety of the trajectory,.
This then transforms our verification problem into the following optimization problem: Is the minimum f(x) for all initial states x greater than zero? This means that we can apply efficient global optimization techniques to great effect in our verification task.
One could argue that such optimization is not verification, that one cannot exhaustively simulate all trajectories and can therefore have no guarantees. One can only use such optimization for refutation. To this, I offer two responses:
First: If one has additional knowledge of the characteristics of one's heuristic function (for instance, Lipschitz conditions or a probabilistic characterization of its class of functions), then an intelligent optimization approach can utilize such characteristics to guarantee a strictly positive minimum with enough testing.
Second: If one has no such knowledge about the heuristic function, then good global optimization is still our best assurance where there is an absence of verification techniques well-suited to most non-trivial continuous dynamics.
With this in mind, let‘s now briefly turn our attention to a comparative study of modern global optimization techniques in order to see which available algorithms are best suited for our purposes and what improvements to such algorithms would be most beneficial.