Math 225 - Differential Equations

Fall Semester, 2009-2010

Go straight to the course syllabus.

A differential equation is an equation involving an unknown function and its derivatives. You have already encountered differential equations in calculus and perhaps in your physics courses. I may be a bit prejudiced, but I think that differential equations are one of the main reasons for studying calculus; in fact, I have even heard it said that differential equations are the raison d'etre for calculus.

Differential equations are important because they often arise when one expresses scientific principles in mathematical terms. Of course, differential equations can be studied in their own right, but it is their connection with real-world problems that makes them so important.

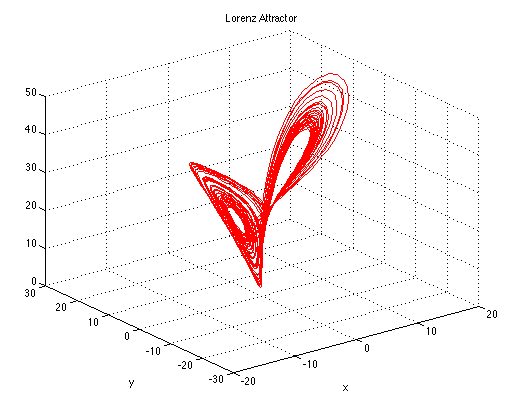
The above picture is a plot of the Lorenz attractor in three-dimensional phase space. We'll be spending a fair amount of time this semester in the phase plane and phase space. Here are two more phase plots. Following the pictures are a few particulars about the course.

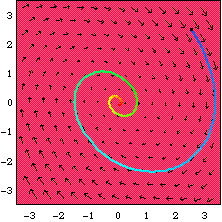
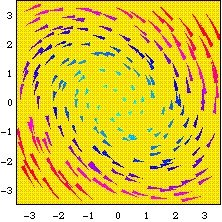
CLASS INFORMATION:

• Meeting time: MWF 9:00-9:50 AM
• Meeting room: Glatfelter 201

OFFICE AND OFFICE HOURS:

• Office: Glatfelter 208
• Office hours: MWF 8:00-8:50 AM, 10:00-10:30 AM, and by appointment

TELEPHONE NUMBER AND E-MAIL:

• Telephone: 337-6630
• E-mail: jfink@gettysburg.edu
• WWW page: http://cs.gettysburg.edu/~jfink/courses/ma225.html

EXAM DATES:

• Exam 1: Wednesday, October 14
• Exam 2: Wednesday, November 18
• Final Exam: Tuesday, December 15

PREREQUISITES:

• Second-semester calculus (Math 112).
• Some knowledge of elementary linear algebra is helpful, but not necessary.

TEXTBOOK:

• Differential Equations, 3rd edition, by Blanchard, Devaney, and Hall
  ISBN 0-495-01265-3

COURSE OBJECTIVES:

• The objectives of this course include:
  • bridging the gap between physical problems and their mathematical formulation by developing the skills of analysis, modeling, and interpretation;
  • honing the skills of problem solving, synthesis, and teamwork;
  • reinforcing mathematical ideas and manipulative skills from calculus courses.
• At times, this blend of activities will be less cut and dry than what you may have come to expect in courses you have taken in the past. Learning to master the uncertainty you will confront in some of the assignments is part of developing intellectual maturity.

COURSE CONTENT:

• Topics from Chapters 1, 2, 3, 4, 5, and 7
• Detailed syllabus

GRADING POLICY:

• Your grade will be determined by your scores on the following:
  • homework (1/6);
  • two exams (1/6 each);
  • project (1/6);
  • final exam (1/3).
• ***There will be no make-up exams and late work will not be accepted.***

DAILY READINGS:

• Assigned readings should be done before class, and you should also attempt a problem or two from the textbook.
• Working problems is essential for an understanding of the material, and there are plenty of problems in the textbook.

HOMEWORK:

• Homework will be assigned, collected, and graded.
• Assignments may include material that will not be discussed in class. You are expected to learn this material on your own and to make use of the resources available to you to complete the assignments.
• Grading will be based both on mathematical content and on the quality of your write-up. NEATNESS COUNTS! Show all work necessary to justify your solutions. Answers alone are not sufficient.
• You may work with other students on the homework; in fact, I encourage that. However, your write-up should be your own.

TEAM PROJECT:

• The project will be a team effort on a topic of your own choice involving an application of differential equations.
• The project is not intended to take an unreasonable amount of time, but it is unlikely that you will complete the project in a single sitting. Thus, your team should begin work on the project well in advance of the due date. You will probably find that shorter work sessions spread over several days are the best way to attack the project.
• To get you started early on the project, a written proposal is a required first step. The proposal is due on Wednesday, November 4.
• Projects will be presented in class at the end of the semester.

COURSE SOFTWARE:

• The computer software we will use this semester includes:
  • MATLAB and associated ODE software developed by John Polking of Rice University.
  • Mathematica.
  • DETools for Differential Equations, the software on the CD that comes with the textbook.